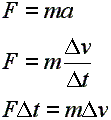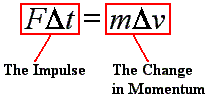Momentum, Kinetic Energy, and Arrow Penetration

(And What They Mean for the Bowhunter)

By

Dr. Ed Ashby

Prologue

To understand the relationship between an arrow’s kinetic energy, its momentum, and their implications towards the ability of a hunting arrow to penetrate tissues, one must rely on the laws of physics. This discussion cannot be made totally uncomplicated. The following is an attempt to impart a fundamental understanding of the applicable principles of physics, as simply as I can, and relate them to the results from actual field data.

Before delving into the deep abyss of the physics involved in arrow penetration, it is appropriate to first take a few moments to discuss the field data, and the logic behind why it is collected in the manner that it is.

Judging from questions I receive, this appears to be a very misunderstood aspect of the study of terminal ballistics. It is, in many aspects, more akin to forensic medicine than to laboratory science. The aficionado of the many forensic medical shows, now so popular on television, will recognize the methodology. One starts with a real event, something known to have occurred, and then uses pure science to determine and explain the “how and why’ of the incident.

Penetration data collected from real shots, into real tissues, is not a static measurement. Outcomes differ from shot to shot, as the uniformity of tissues encountered change. In the real world it is impossible to control all the variables, and one does not wish to do so. Those variables do exist. They will be encountered.

The scholar of abstract science will cite that this testing methodology includes too many variables, but it is precisely because of the multitude of variables that it is necessary. When dealing with infinitely complex variables, only ‘outcome driven’ information analysis, from a multiplicity of data, provides usable results. This is why the medical community commonly uses ‘outcome driven’ studies.

A commonplace example of these differing test approaches occurred with the development of automobile air bags. Engineers did enormous static testing with crash dummies, controlling all variables, before air bags were introduced.

After the introduction of air bags into production automobiles, outcome driven analysis showed that significant numbers of adult humans were being injured, and sometimes killed, by air bags during their deployment. An even larger number of children were being injured or killed. Static testing had indicated the deployment force would be safe. The ‘reality’ outcome was not as the static testing had predicted.

Outcome studies of air bag performance, in real automobile crashes, with real people on board, pinpointed the incidences where both serious and fatal damage was caused to humans by the air bag. It delineated the tendencies; when the events were likely to occur.

The static test standard was a male, of 160 pounds weight, seated normally within the car. Observed injuries and deaths occurred when occupant size was below the ‘average size’ that had been used in the static studies to determine the safe force levels exerted upon the various parts of the body during air bag deployment AND when the occupant was located closer to the air bag at time of deployment than the ‘static testing standard’ (as with persons using a cushion or pillow behind their back while driving or riding).

The frequency of occurrence of these events was tracked in the outcome studies, and found to have a significant prevalence. Then researchers turned to the pure sciences to find the explanations for the events, which had now been shown to occur in the real world. Force of impact, in relation to both occupant size and position at time of impact, was the culprit.

The force of air bag deployment was simply too violent for human tissues, under particular sets of circumstances, which did occur in the real world application of the air bags. The force of air bag deployment was modified. Outcome analysis of air bag deployment force continues today, and the regulations and guidelines are still being modified, based upon outcome driven studies.

The above example pinpoints the major differences in methodology between the measurements of pure laboratory science and the outcome driven method of deriving conclusions. In laboratory science, one starts with pure measurements and tries to predict future events. Outcome driven studies start with events known to occur; then looks for the scientific explanations of how and why it occurred.

Outcome driven studies factor in the probability of occurrence when a large number of independently acting variables are randomly introduced into the observed results. Another way of saying this is that outcome driven studies include the Murphy Factor; to find out what can happen; when it is likely to happen; and how often it actually happens.

Another major difference between laboratory science and outcome driven studies is that outcome driven results have an ‘acceptability level’. Their validity does not have to meet any level of ‘engineering credibility’; the ability to be repeated at will, each and every time.

For example, how many ‘unsuccessful outcomes’, deaths or injuries, caused by an air bag’s failure to perform as intended, are required before it is deemed as ‘unacceptable performance’ under the real conditions of use? This question is even more valid when the identified cause of the incidences is easily preventable.

The gravity of an incident; the tendency for it to occur under particular circumstances; the frequency with which its actual occurrence is observed; and society’s morals all determine the level of acceptability. So, one has to ask, “What is the acceptable level of failure for a hunting arrow to perform as expected in tissues?” As a bowhunter, I am interested in outcome; outcome in tissues, not in a homogeneous test medium. I think most bowhunters are!

For many years I tried to find a test medium that would give results which correlated to the observed incidents which occurred under field conditions, as a hunting arrow penetrated real tissues. Such a test medium would make the investigation of terminal ballistics of hunting arrows very much simpler, and far less time consuming and expensive.

Ballistic gel, covered with a suitable elastic outer covering, gives a reasonable correlation to tissue hits in which no hard tissues are encountered, but I have found no combination of materials that will correlate with the multiplicity of resistance forces encountered in penetrating real tissues. This past year, a European forensics team also tried to find a synthetic testing medium that would give results comparable to that seen in real arrow wounds. They also found none.

An absolute ‘predictor’ of arrow penetration, on every shot, is impossible. Outcome driven analysis from real shots, into real tissues, does, however, give a definitive picture of any given arrow’s incidence, tendency, and frequency of occurrence of events during tissue penetration. Testing in a uniform medium does not. Having tried both approaches, I feel certain that it is only through the use of outcome driven results that reliable indicators of an arrow’s likelihood of performance under real hunting conditions can be developed.

Before launching into the physics of arrow penetration, we first need some basic definitions. Those not ‘technically predisposed’ will find the first part tedious, but it is necessary groundwork for one to understand the propositions that follow. It is important for one to know that the recommendations are grounded in both the coherent logic of physics and the empirical facts; facts confirmed through nearly a quarter century of intensively collecting and collating detailed field measurements of the terminal performance of hunting arrows in real animal tissues.

[NOTE: For the benefit of those who find the ‘highly technical’ difficult, some of the more ‘technically precise’ clarifications and information has been set aside in text boxes, and denoted as a “Nerd’s Note”. (Nerd: Defined as an enthusiast whose interest is regarded by others as too technical or too scientific. Somehow, I think I resemble that remark!). It is entirely acceptable for those ‘mathematically challenged’ to omit reading the Nerd’s Notes! Their omission will not affect the reading of the other text.]

The Laws of Physics

FORCE: Force is defined in physics as that which tends to change the momentum of a body containing mass. Force is proportional to the rate of change of momentum.

Nerd’s Note: Force (lbf) = [mass (lbm) times the acceleration (expressed in ft/sec²)] divided by the gravitational constant. The gravitational constant is 32.174 lbm-ft/lbf-sec², and is abbreviated as ‘g_c’. In English units, the g_c is used anytime one goes from pounds mass (lbm) to a force, (lbf).

MASS is a quantity of matter, and is expressed in ‘pounds of mass’, (abbreviated as lbm). Weight is the force exerted on an object due to the gravitational field, and expressed in pounds of force (abbreviated as lbf). In physics, mass (‘lbm’) is expressed as the weight of the object (in pounds force) multiplied by the gravitational constant and divided by the force of gravity. Though the numerical value of an object’s mass and weight can be the same, the units of measure and theory behind them differ.

Nerd’s Note: Weight (or the force as a result of mass) has the following equation when using English Engineering Units:

W(lbf) = [mass(lbm) * g (32.174ft/ sec²)/g_c (32.174 lbm-ft/lbf-sec² ), or, to conform to the above,

Mass (lbm) = W (lbf) * g_c/g

Note: The factoring in of the g and g_c does not change the resultant value; it just makes the units consistent. This becomes a factor anytime one talks about, or calculates, “force” and its effects, as it distinguishes clearly between the mass of an object and the force applied by the mass.

MOMENTUM: The unit of measurement for momentum is slug-feet per second. A slug is a portion of the subset of coherent units known as the gravitational foot-pound-second system. The physical weight of one slug of mass equals 32.174 pounds. One slug of mass will acquire an acceleration of one foot per second per second when acted on by a one pound force (at sea level).

Nerd’s Note: Momentum can also be expressed in lbf-sec, if one is not using the slug as the unit of measure. The slug has units of lbf-sec²/ft. It is essentially mass (lbm) with the g_c already divided into it.

A body of mass (M) moving at a velocity (V) has a momentum equaling M x V. This says, “The momentum equals the mass of the object [expressed in pounds of mass (lbm) and divided by the pull of gravity, which will result in the mass of the object in slugs], times the velocity [expressed in feet per second] at which the mass is moving”.

Momentum has both amplitude (an ‘amount’ value) and a direction. Because any measurement of momentum has a specified direction it quantifies the net force acting in that single, straight line, direction. Momentum is, therefore, known as a linear function, and is a measurement of the force of forward movement of an object.

Nerd's Note: While there are situations where momentum can also be angular, in dealing with penetration the use of linear momentum is the simplest and most applicable method.

VELOCITY is defined as the change in position divided by the time period during which the change occurs. It is expressed in units of distance per unit of time - or, for our purposes, in “feet per second”.

ACCELERATION is the rate of change of speed, or how much the velocity of a body in motion changes during a specified period of time. Consequently, the acceleration of gravity is expressed in “feet per second per second”. This quantifies how many feet per second the velocity changes as each second passes.

IMPULSE: Force (in our case, the momentum) applied over a unit of time creates an impulse.

The concept of impulse is extremely important in the study of momentum, and to the understanding of arrow penetration. Time passes as a force is applied to an object. When this happens we say that an impulse is applied to the object.

When a bow launches an arrow, an impulse is applied to the arrow. The bow applies a force on the arrow for a short time period. According to Newton's third law of motion, forces always come in pairs. Thus, the arrow also puts a force on the bow, and the bow, therefore also has an impulse applied to it.

NET FORCE is the total amount of force exerted by a body in motion. It is the change in momentum divided by the change in time.

When the mass of a moving object remains constant, as with an arrow in motion, the net force equals the mass (in slugs) times the change in velocity divided by the time period over which the change occurs. By definition, the change in velocity divided by the change in time gives the acceleration of a moving body. Therefore: when the mass of a moving body remains constant the force will equal the Mass (in slugs) times the Acceleration. (Force equals mass times acceleration. In equation form this is expressed as: F = ma).

Nerd's Note: When using English units, rather than slug mass, this equation would be expressed as F = ma/g_c or, if one prefers, F = (m / g_c) * a. This is necessary to convert from lbm to lbf.

It is essential to understand that any reference to the net force of a moving object is specific to the specified time period being referenced. In one set of circumstances, net force can equal the total disposable force of an arrow in motion. In another reference, net force can imply the remaining force after deductions, as in calculating the net force remaining after an arrow completely penetrates an animal.

When an arrow’s net force after penetration (at the time of exit) is deducted from the (total disposable) net force of the arrow at the time of impact it equals the amount of the arrow’s disposable net force that was required for the arrow to completely penetrate the animal on that particular shot. That amount of the disposable net force available to the arrow at impact was expended over the time period required for the arrow to pass through the tissues.

IMPULSE: An impulse is equal to the net force of the object times the time period over which the force is applied. The impulse equation is mathematically derived from the equation F = ma, which comes from Newton’s Second Law of Motion. Study the following. It shows the derivation of the impulse formula.

Line 1: Force equals mass times acceleration. Line2: Substituting the definition of acceleration for “a” in the equation. Line 3: Algebraic rearrangement. The force multiplied by the change in time equals the mass multiplied by the change in velocity.

The first line is our familiar equation F = ma.

The second line expresses the acceleration by its basic definition, a change in velocity divided by the change in time.

The third line is arrived at through algebra, by multiplying each side of the equation by delta t (which is the symbol for change in time), canceling it on the right, effectively moving it over to the left.

Nerd's Note: If working in English units, one must not forget to factor in the g_c constant to change from pounds mass (lbm) to pounds force (lbf) in the above equations, When doing so, the first line of the equations above would be: F=ma/g_c

The left side of the third line is called the impulse on the object. That is, impulse is equal to the net force times the length of time over which that force is applied. The right side of the third line is called the change in momentum. Thus, the impulse equals the change in momentum.

The Impulse equals the change in momentum

An arrow in motion has a mass of M and is moving at a velocity of V. As a result the arrow possesses a predetermined momentum (mass times velocity) at the instant of impact. When the arrow strikes an animal it will decelerate (a negative acceleration value).

If the arrow stops in the animal it will have expended the entire disposable net force available to it at the instant of impact over the time period required for it to come to a full stop. A resistance impulse force equaling the arrow’s disposable net force at impact will have been applied by the tissues upon the arrow, and it will have occurred over the exact same time period.

In this situation the arrow’s velocity change is 100%. The momentum of the arrow at impact, divided by the time period required for the arrow to come to a complete stop, will equal the impulse of the arrow upon the tissues. The resistance force of the tissues to the arrow's passage during the time required for penetration represents the impulse of the tissues upon the arrow. The two impulses will be equal. The time factor will be equal between the two impulses. The force of momentum and resistance force will be equal.

If the arrow passes completely through the animal, the applied impulse equals the arrow’s momentum at impact minus the arrow’s retained momentum at exit, for the time period required for the arrow to pass through the tissues. As the mass of the arrow remains constant during the entirety of its passage through the tissues, the arrow’s net force decreases only in proportion to the amount of velocity loss during the course of penetration.

Given two arrows of equal momentum, but with one deriving a greater portion of its momentum from mass than the other, the heavier arrow will change velocity (decelerate) at a slower rate as it passes through the tissues. In other words, the heavier arrow will retain a higher percentage of its impact velocity at any given time period during its passage through the animal’s tissues, thus it also retains a higher momentum at any given point during the time required for the arrow to penetrate.

Another way of saying this would be that, though the heavier arrow is traveling slower, it takes a longer time to stop. The result is that the heavier arrow will have a greater impulse of force than does the light arrow.

It is momentum that gives an object in motion the tendency to STAY in motion. The greater the contribution of the object’s mass is to the resultant momentum the harder it will be to stop the forward progression of a moving object. Anyone who has pushed a car in neutral and then tried to stop it will understand this. The more of a moving object’s momentum that is derived from its mass, the more TIME it takes to stop it with any given resistance force.

It is common for proponents of light and fast arrows to counter that the faster arrow will have traveled a greater distance through the tissues in the same time period than will the heavier, and slower, arrow. This would be valid were it not for the nature of resistance forces.

As the arrow’s velocity is increased the resistance does not increase equivalently. The resistance increases exponentially. The resistance of a medium to penetration is reliant on the square of the object’s velocity (assuming objects of a given coefficient of drag; i.e., using arrows with the same external profile, material and finish). In other words, if the arrow’s impact velocity doubles, the resistance increases by a factor of four. If the impact velocity quadruples, the resistance to penetration increases 16 times!

The effect of exponentially increasing resistance is easy to experience. Try holding a hand out the window of the car, while the car is going at a velocity of 30 miles per hour (which is only 44 feet per second), and feel the air’s resistance against your hand. The resistance is very slight. Now accelerate to 60 miles per hour (a mere 88 feet per second). The velocity has only gone up by a factor of two, but the air’s resistance to your hand passing through it is now four times greater.

Now imagine the effect on an arrow passing through tissues. Tissues are more solid than air. They have a greater density. Their resistance to an object’s passage is higher. Visualize the effect as an arrow’s velocity increases from 150 feet per second (a fairly typical velocity from a mid-draw weight traditional bow) to 300 feet per second (as from a top line compound bow).

Let us now assume an arrow weighing 700 grains for the slower bow (150 fps is easily achievable with that weight arrow and a ‘traditional’ bow) and a 390 grain arrow for the faster bow (the advertised velocity rating for one of the newest compound bows on the market, using that weight arrow). The slower arrow has 0.466 slug feet per second of disposable net force. The faster arrow has 0.519 slug feet per second.

Lets also assume these two arrows are of same materials, have equal physical external dimensions (easily achievable), and both have perfect flight characteristics. The tissue’s resistance increase is totally dependant upon the velocity of the arrow.

The lighter arrow has 10.22 percent more disposable net force (and 123.2 percent more kinetic energy) than the heavier arrow but, because of its higher velocity, it is met by four times the resistance to penetration. Which arrow will penetrate further in real tissues? Empirical evidence from the outcome studies provides an overwhelmingly definitive answer. Both the frequency and degree to which the heavier, slower, arrow out-penetrates the lighter one is of such a magnitude that it must be viewed as the norm.

ALL MOMENTUM IS NOT THE SAME

Given two arrows, identical in shaft and broadhead materials and profile, and having EQUAL momentum, but possessing UNEQUAL mass, the arrow deriving the greater portion of its momentum from its mass will penetrate better. The Laws of Physics requires this to be true, and ALL of my field test data validates this to be the case.

To say this in another way, arrow momentum derived through increasing arrow mass results in a greater gain in penetration than does momentum gained by increasing an arrow’s velocity. This is true because the tissue’s resistance is increased by the square of the velocity.

Let’s look at two arrows of equal momentum, but unequal mass, both of which expend all their available net force in the tissues. If the momentum is equal between two arrows at impact, the one with the greater mass has to be traveling at a slower velocity. As shown above, the slower arrow will be met by a lower resistance force than the faster arrow.

With the momentum of the two arrows equal at impact, their disposable net force will be equal, but the resistance force will be greater upon the faster arrow. Because of the higher resistance force, the faster/lighter arrow will lose velocity more rapidly, and its momentum will diminish at a faster rate than that of the heavier arrow. It will stop in a shorter period of time, thus it will have a lower impulse of force than the heavier arrow.

To quantify the potential for penetration we must first quantify ALL the directional FORCES involved.

KINETIC ENERGY: When an object is in motion, it has kinetic energy. Kinetic energy is defined as the total energy of a body in motion. Kinetic energy is scalar, or non-directional, in nature - it is the TOTAL energy, of all types, in all directions. That is: kinetic energy has magnitude, but it does not have direction. (Note that kinetic energy is defined as ENERGY, not as FORCE.)

Kinetic energy includes all the types of energy of a body in motion, and is very dependent on the object’s velocity. When a moving object with mass strikes something, the kinetic energy is transferred, as one or another form of energy.

An arrow’s kinetic energy at impact is the basic ‘potency’ of the collision - how hard the arrow strikes the target. Kinetic energy is measured in "foot pounds". A 'foot pound' is the amount of energy needed to exert a one pound force for a distance of one foot. (Note that foot pounds is a measure of the energy required, not a measure of the force itself). Force is a portion of the arrow’s total energy.

The formula for kinetic energy is: Kinetic energy equals one half the mass (lbm) times the velocity squared and divided by the gravitational constant (g_c).

Kinetic energy is often cited by the advocates of light weight, high velocity, arrows as the standard for predicting an arrow’s ability to penetrate. But consider a baseball.

A baseball weighs 5.12 ounces (that’s 2240 grains) and can be thrown in excess of 95 mph (which is 139.33 feet per second). It has 96.5 foot pounds of kinetic energy. It actually strikes much harder than a heavy hunting arrow at ‘traditional bow’ velocities, but I can't really see hunting buffalo with a fast ball! Kinetic energy determines how hard the baseball strikes; it has no direct bearing on how well it penetrates.

As with the baseball, a tuning fork, once struck, has high kinetic energy (it can shatter a crystal wine glass), but has almost no momentum. It would make a darn poor weapon against an animal of even modest size!

The kinetic energy of a moving arrow includes ALL the energy, of all types, inherent to the arrow. This includes such things as the flexional energy; vibrational energy (some of which is transformed into the sonic, or sound, energy); all of the rotational energies; gravitational energy; potential energy; and the heat (frictional) energy generated by its passage.

An arrow’s momentum is also a part of the arrow’s kinetic energy - the only part that relates to its ability to penetrate. Some of an arrow’s kinetic energy is dissipated as other forms of energy during flight and on impact. Even the ‘sound’ of a hit is derived from the arrow’s kinetic energy.

As shown above, the Laws of Physics dictates that momentum, and not kinetic energy, is the correct unit of measure to quantify the linear (straight line) "potential disposable net force" that is available to an arrow. Momentum determines THE AMOUNT OF FORCE which an arrow has available to it for penetration.

(Perhaps this is a good point at which to digress for a moment. Kinetic energy is frequently used as a guide to the potential lethality of a high speed bullet. This is because a bullet can cause tissue damage in ways an arrow can not.

Bullets carry massive amounts of kinetic energy, relative to an arrow. Much of a bullet’s kinetic energy is transferred through the tissues as a ‘shock wave’, caused by the rapid compression of tissue fluids.

As the bullet strikes, a ‘hydraulic force’ is transferred, through the tissue fluids, over a wide area. This causes histologic tissue shock, disrupting tissue functions. It is this hydraulically induced ‘shock wave’ that causes the ‘bruising’, or ‘blood-shot’ tissues surrounding a bullet induced wound channel.

If one researches the literature of terminal ballistics and killing power of firearms, they will find that, even there, the use of kinetic energy as an indicator of bullet lethality falters badly as the size of the animal increases. Its usefulness also diminishes with firearms producing low (by firearms standards) kinetic energy, as with handguns. This is the reason that such other ‘indicators’ of bullet lethality as “Taylor’s Knock-Out Value”, the “Optimum Game Weight” and the “Power Factor” find their way into firearms literature, all of which place more emphasis on the bullet’s momentum and/or impulse of force.

Studies conducted by the U. S. Army’s Ballistics Research Facility indicate that tissue shock from hydraulic compression becomes a significant “wound factor” only at impact velocities around 2500 feet per second, or greater. Creating ‘hydraulic shock’ is not an option with an arrow).

Kinetic energy is NOT the correct unit of measure for calculating ANY of the forces relevant to penetration. It is applicable for calculating neither the force of a moving object; the disposable net force at impact; the net force at exit; net force consumed during penetration; the applied impulse; nor the resistance impulse force affecting penetration.

With a given arrow, if its kinetic energy is increased, there will be a measurable increase in its penetration, but only because the velocity increase necessary to achieve more kinetic energy has also increased the arrow’s momentum. The increase in penetration will not be proportional to the increase in kinetic energy. It will be proportional only to the resultant increase in the arrow’s momentum (with the increased resistance created by the higher velocity also factored in).

Kinetic energy IS applicable for calculating the mechanical efficiency of one’s bow.

Efficiency is defined as the ratio of the amount of energy (Ah, now we get to use ENERGY) used by a machine to the amount of useful work done by it.

A “machine” is defined as a device with moving parts used to perform a task. Work is defined as the transfer of energy, measured as the product of the force applied to a body multiplied by the distance moved by that body in the direction of the force. Work is force times a distance. Work can also be defined as being equal to the change in kinetic energy.

For a bow and arrow system, the bow’s efficiency is defined as the proportion (percentage) of the bow’s stored energy that is transmitted to the arrow when it is fired. The more efficient a bow is the higher will be the amount of its stored energy (i.e., the potential energy that is stored in the limbs of the drawn bow) which is transferred to the arrow when the bow is fired.

The arrow’s kinetic energy is derived directly from the ‘output kinetic energy’ of the bow, and represents the useful work performed by the bow. The arrow’s momentum will be a function of the bow’s output kinetic energy and the arrow’s mass, but it is not the product of them. (In mathematics a “function” is a quantity whose value depends upon the varying values of other quantities, while the “product” is the result of the multiplication of two or more quantities.)

When one looses and arrow, a portion of the bow’s stored potential energy is used to apply a force upon the arrow. The applied force acts upon the arrow over the time period during which the arrow remains on the string.

This force, applied over this time period, will be the impulse of the bow upon the arrow. It is this applied impulse which causes the movement of the arrow’s mass. In other words, it changes the velocity of the arrow, and the arrow’s mass times its launch velocity determines the arrow’s momentum at the instant it departs from the bowstring.

A bow’s output kinetic energy allows one to estimate the bow’s ability to cast an arrow. The greater a bow’s output kinetic energy, the more capable it is of casting a heavy arrow with acceptable levels of velocity and trajectory for ethical hunting ranges.

Thusly, the output kinetic energy OF A BOW is a useful INDICATOR of how much arrow momentum it can produce.

Impulse is the FORCE applied by a body in motion, over a period of time, upon the object it hits. Momentum has FORCE. Kinetic energy has ENERGY. An arrow’s net disposable force equals its momentum at the instant of impact, and must be met by an equal resistance force, acting over the time period of the impulse, for the arrow to come to rest.

Kinetic energy does not enter directly into any of the calculations relating to penetration. THE KINETIC ENERGY CARRIED BY AN ARROW AT IMPACT HAS NO DIRECT BEARING ON ITS ABILITY TO PENETRATE.

If one fills a 5 gallon plastic pail with sand and fires both a .357 magnum and a heavy hunting arrow at it, the bullet will be stopped by the sand, while the arrow will penetrate the pail completely. The .357 magnum handgun has a 158 grain bullet traveling at 1250 fps, for a momentum of 0.83 slug-feet per second, and a kinetic energy of 520 foot-pounds. A 710 grain arrow at 183 fps has only 0.57 slug-feet per second of momentum, and a mere 52 foot-pounds of kinetic energy.

These are actual combinations I have used to demonstrate the penetration power of a heavy hunting arrow. Our baseball, with 96.5 foot pounds of kinetic energy, and 1.39 slug-feet per second of momentum, will simply bounce off. What makes the difference?

A major factor between the bullet and the arrow is the increased resistance force met by the higher velocity bullet. While the bullet has ten times more kinetic energy, and 37.5% more momentum, than the arrow, its almost seven times higher velocity causes the bullet to be met by nearly fifty times as great a resistance force as that encountered by the arrow!

Another major factor between the handgun’s bullet and the arrow (yes, we will get to the baseball shortly) is the longer time period of the arrow’s impulse; which results from its higher mass. Though the arrow is traveling much slower than the bullet, and has less momentum than the bullet, it derives a greater percentage of the momentum it does possess from its mass. It is ‘heavier’.

The heavier (and lower velocity) arrow “decelerates” more slowly than the bullet or, if one prefers, it has a longer time period over which the force acts. Remember? Force multiplied by the time it acts equals the impulse. The heavier arrow retains a higher percentage of its force for a longer period of time than does the bullet. The bullet’s total net disposable force, though very high relative to the arrow, is entirely dissipated in milliseconds.

Now, to our baseball. Our pale of sand also has a differing resistance to the passage of projectiles having differing cross sectional areas and profiles.

The baseball has a much larger surface area presented to the bucket, in relation to its mass, than does the bullet. The bullet presents a larger surface area per unit of mass than does the arrow. In physics this difference in the ‘penetration ability’ is defined by the sectional density of the object.

The SECTIONAL DENSITY of an object of round (cross sectional) profile is defined as the mass of the object divided by the square of its diameter. The heavier the object is in relation to its cross sectional area, the higher its sectional density. The higher the sectional density, the less the amount of frontal surface area (per unit of its mass) that is presented to the target, and the less of the target’s ‘matter’ (relative to the penetrating object’s mass) that will be displaced by the passage of the object through the target. This translates into a lower level of resistance on the frontal area of the projectile.

If the mass of an arrow is increased without changing its external dimensions, it will weigh more per unit of cross sectional area. Its sectional density will be increased, and it will penetrate farther with any given applied force.

Note that the sectional density refers only to the resistance on the penetrating object’s frontal area and the amount of ‘matter’ displaced in relation to its mass. In tissues, an arrow’s “shaft drag” is also an important feature influencing penetration. Shaft drag results from the frictional forces between the arrow shaft’s surface and the substance being penetrated.

Shaft drag is one major reason that arrow penetration test into artificial test media often differs from actual results derived from testing on real animal tissues. Most ‘target materials’ rely heavily on shaft drag to stop the arrow. They are made from materials specifically chosen and designed to ‘close down’ around the shaft, exerting the maximum possible shaft drag. Muscle fibers, on the other hand, tend to retract, actually spreading apart, when cut by a sharp broadhead.

When cut, muscle tissues also release blood, which lubricates the shaft, reducing the coefficient of friction between the arrow shaft and the tissues. This reduces the drag on the shaft. These biologic reactions are a major reason why accurate and reliable measurements of hunting arrow penetration can only be achieved through testing conducted on live (as when actually hunted) animals, or VERY freshly killed animals.

Even when testing on freshly killed animals, physiological tissue changes occur rapidly, and testing must be done within minutes of death. If the time lag is longer, results become erroneous, due to changes in tissue resistance forces encountered.

Yet another difference in the ability of hunting arrows to penetrate tissues, as opposed to bullets, is that they are tipped with a broadhead. Yes, the broadhead slices through tissues, rather than having to ‘push’ through them, but there is more.

A broadhead is a “simple machine”, a series of inclined planes. These inclined planes allow the arrow to accomplish more work with any given applied amount of force. The profile of the broadhead offers a mechanical advantage.

MECHANICAL ADVANTAGE: Mechanical advantage is defined as the improvement gained by use of a mechanism (machine) in transmitting force (There’s that word again!). Specifically, it is the ratio of the force that performs the useful work of the machine to the force that is applied to the machine. In other words, broadhead design can multiply the force of the arrow, increasing its ability to do work.

Not all broadheads offer an equal mechanical advantage. As with any inclined plane, the longer the slope of the plane in relation to the rise of the plane, the higher will be the mechanical advantage.

A long and narrow single blade (2 cutting edges) broadhead will have a higher mechanical advantage than one of equal length and width, but having more blades. Also, as the profile of a broadhead’s blade(s) becomes shorter and/or wider the mechanical advantage becomes lower. Having either a convex or concave cutting edge profile, rather than a straight taper, also lowers a broadhead’s mechanical advantage.

Any abrupt rise in the contour of a broadhead results in a profile which lowers the broadhead's mechanical advantage. This is why a very smooth and gradual fade-in of the broadhead’s ferrule into the blade is important in broadhead design. It detracts less from a broadhead’s mechanical advantage.

In trying to maximize arrow penetration, there is also the efficiency of the bow/arrow system to consider. Up to the limits of the bow’s ability to move the arrow, bows become more efficient as the mass of the arrow increases.

A heavier arrow causes a bow to shoot more quietly than with a lighter arrow. This is because of the increased efficiency. More of the bow’s stored energy is transmitted to the arrow and less is ‘wasted’ in the form of bow vibration, which causes increased hand-shock and noise. Increasing bow efficiency through the use of greater arrow mass results in both a quieter shooting bow and one which imparts more force to the arrow. A win-win situation for the bowhunter.

For almost a quarter century I have been actively collecting terminal arrow performance data from shots into real animal tissues, and have the world’s most extensive ‘real tissue’ arrow wound database from which to extract comparative outcome information. All empirical data supports the conclusion that the above laws of physics apply to hunting arrow penetration in tissues.

In real tissues, it is easy to get a very light, very fast, arrow combination, generating high amounts of kinetic energy, which averages significantly less penetration than an appreciably heavier arrow producing only one third as much kinetic energy. A high frequency of this outcome is demonstrable; with both arrows having identical broadheads and the same shaft materials and dimensions.

What does all this mean for the bowhunter?

Let’s try to put everything into context. Relative to virtually all big game hunting weapons, hunting arrows have a very low amount of force available with which to do their job - penetrating animal tissues.

Lack of penetration is the number one cause of a hit being non-lethal. The terminal arrow performance data from each and every one of my studies overwhelmingly verifies that fact (and the data is of sufficient magnitude that it must viewed as fact, at least until data of an equally substantive nature, derived from outcome testing on real animal tissues, demonstrates any reason to believe otherwise).

If one wishes to maximize the hunting arrow’s ability to penetrate then consider the following.

(1) Maximize the bow’s efficiency. That means shooting the heaviest arrow one can while still maintaining a trajectory that is adequate for ethical bowhunting ranges.

Most bows show a rapid increase in efficiency with increasing arrow mass up to the point of approximately 12 to 14 grains of arrow mass per pound of bow draw weight. (The exact point where the rate of efficiency increase begins to decline varies from bow to bow and shooting style to shooting style. There are many variables, and the value of a chronograph to the shooter should not be underestimated.) Beyond this point of arrow mass per pound of bow draw weight a bow’s efficiency will still increase as the arrow gets heavier, but the rate of efficiency increase slows down.

(2) Use broadheads of high mechanical advantage. This becomes increasingly important as the bow’s draw weight becomes lighter, or the size of the animal being hunted becomes larger.

Use of a high mechanical advantage broadhead also becomes increasingly important as the power stroke (the distance the arrow travels before it leaves the bow string) becomes shorter. A shorter draw length gives a shorter power stroke, which also means that, regardless of the amount of force stored in the bow’s drawn limbs, that force will be exerted upon the arrow for a shorter period of time.

For any given amount of applied bow force, the longer one’s draw length, the more time the bow has to exert its force upon the arrow; i.e.; the bow’s impulse upon the arrow will be greater, and the bow’s efficiency increases. (Force applied over time equals the impulse.)

(3) Use broadheads with a cut-on-impact tip. Broadheads of a cut-on-impact tip design penetrate soft tissues with less resistance that other broadhead tip designs. The various tip designs, and their effects on penetration in bone, are still under investigation in the current study.

(4) Accept nothing less than perfect arrow flight in your hunting arrows. It minimizes energy loss during the arrow’s flight, and reduces resistance forces on entry (due to less shaft flexion), which results in the arrow retaining more force to apply directly to penetration.

Achieve perfect arrow flight through wise selection of arrow shafting materials and spine, perfect broadhead-to-shaft alignment, careful bow tuning and the use of sufficient fletching to stabilize the arrow in flight.

Start with a really good broadhead and then set your hunting arrows, and your bow, up around the broadhead. In testing I have used a couple of hundred different types and designs of broadheads. As long as the broadhead is aligned so that it spins in precise balance, on a straight shaft, I have yet to meet ANY broadhead that I cannot get to fly perfectly. This applies even to stone points! The ‘balance’ of the broadhead does not have to be perfect. The ‘balance’ of the arrow system does!

[Tip: If the broadhead spins true, and the shaft is correctly spined to the bow (for that weight broadhead), and it is straight, yet the arrow still ‘wind planes’, there is not enough fletching to overcome the wind shear effect created by the broadhead’s blades as they rotate through the air. To stabilize the arrow in flight, use more fletching surface area. This is especially important when the broadhead itself is not well balanced; presenting surfaces with varying shear angles to the air, such as with a stone point.]

Once you have your hunting arrow flying perfect, make your practice arrows (be they for target, field, small game, roving or stump shooting) shoot just like your hunting arrows, not the other way around! It is foolish to sacrifice good broadhead construction, profile and mechanical advantage just to get one’s hunting arrows to ‘shoot just like a target arrow’.

[Tip: A well tuned bow/arrow combination will shoot ALL equal weight broadhead/field tip/target points into the same group at any range. If the point of impact is different between field tips and broadheads of matching weight, there is a ‘tuning’ problem.]

The hunting arrow is the single most important piece of equipment that the bowhunter carries afield. The broadhead chosen is the most important part of the hunting arrow.

A hunting bow merely launches the hunting arrow. The arrow delivers the broadhead. When the broadhead hits it must perform, without failure, each and every time. To do otherwise risks a wounded animal and failure of the entire hunt.

A perfectly placed hit can frequently be non-lethal when there is a failure of the broadhead tipped hunting arrow to perform its task; penetrating and disrupting the body’s life support functions.

(5) Mechanical Broadheads. Mechanical broadheads have become very popular in recent years. Mainly this has occurred because it is extremely easy to get them to shoot much like a target or field point of equal weight, even when the arrow’s fletching area is insufficient to stabilize a fixed blade broadhead. In flight, mechanical broadheads present less surface area to the air. They have a lower wind shear effect.

Mechanical broadheads do, however, encounter significant resistance upon opening in tissues. Outcome studies show that they require a substantially higher level of impact momentum to achieve the same amount of penetration as a broadhead of a more ‘traditional’ design.

This needless loss of disposable net force reduces penetration. Remember? Outcome studies show that lack of penetration is the number one cause of a hit being non-lethal and, in all testing to date, mechanical broadheads average less penetration, on an arrow of a given mass and momentum, than does either a replaceable blade broadhead or a more 'traditional' broadhead of comparable mechanical advantage.

In addition to their needless loss of disposable net force during blade deployment, mechanical broadheads pose some other penetration problems. All of the many mechanical broadheads thus far examined in field testing have a low mechanical advantage. As the field data shows, this further inhibits penetration capability when tested on real animal tissues.

In all testing to date, mechanical broadheads have also suffered by far the highest damage rate of all categories of broadheads tested. The outcome data manifestly shows that a broadhead which becomes damaged during the course of penetrating an animal causes a dramatic increase in resistance, and penetration is severely decreased.

It is highly likely that the high damage rate to the blades of mechanical broadheads results from the abrupt increase in resistance encountered at the time of blade deployment. Though the total amount of resistance force encountered by the blades may not be any greater than that encountered by a fixed blade broadhead, a major portion of the resistance force is encountered over a very short time period; abruptly upon deployment. This ‘spike’ in resistance force must be met by utilization of a higher proportion of the arrow’s disposable net force; reducing the arrow’s retained disposable net force, which, in turn, lowers the arrow’s overall impulse of force upon the tissues.

Fixed blade broadheads enter the tissues with blades fully deployed. They can utilize any mechanical advantage they do have from the instant of impact, i.e.: the mechanical advantage is available to them in penetrating the very elastic skin. Mechanical broadheads cannot use the mechanical advantage of their blades until after the blades are deployed.

The skin’s property of elasticity imparts a ‘give’ to them as the arrow hits. This can drain off substantial amounts of an arrow’s disposable net force. This ‘give’, when an arrow impacts, is why a loosely hung carpet makes a pretty fair arrow backstop. More ‘work’ is required of the arrow to penetrate the carpet. Remember? Work is force times distance. The resistance force has to be moved over a greater distance by the arrow’s impact force before the arrow penetrates.

It is because less work is required for them to penetrate the skin (and the other soft tissues) that broadheads with a cut-on-impact tip penetrate better in soft tissues than do broadheads having other tip configurations. The bevel of the tip’s cutting edge is also an inclined plane - a simple machine. It, too, offers a mechanical advantage.

The longer the bevel (the lower the sharpening angle), the higher the broadhead tip’s mechanical advantage will be. But there is a lower limit. The tip MUST be strong enough to resist damage upon impact with hard tissues (bone). A broadhead that becomes damaged during penetration dramatically increases resistance, and overall penetration suffers.

Though mechanical broadheads having a cut on impact tip permit easier penetration through the very elastic skin tissues, thus far there has been little outcome difference, on comparable shots, in the measured overall penetration (relative to mechanical broadheads having other types of tips and offering a similar mechanical advantage). This is suggestive that energy loss at the time of blade deployment is a major factor in the reduction in tissue penetration measurable with mechanical broadheads.

(6) Arrow Shafts. With any given shafting material and shaft finish, the larger a shaft’s diameter the greater will be the resistance to its penetration. It will present a larger frontal area to the tissues, displace a greater volume of tissue as it penetrates, and present more total surface area to the tissues (which results in a higher drag factor).

As a general rule, the arrow’s shaft should have a diameter that is less than the broadhead’s ferrule diameter. In testing with parallel shafts (as opposed to tapered or barrel tapered shafts), outcome data shows that when a shaft’s diameter is greater than the broadhead’s ferrule diameter the arrow’s penetration is reduced by and average of 30 percent, as compared to a situation where the shaft’s diameter equals the diameter of the broadhead’s ferrule.

If the shaft’s diameter is less than that of the broadhead’s ferrule, the penetration increases by an average of 10 percent. That can equate to as much as a 40 percent difference in measurable penetration between two arrows which are equal in all respects except for the diameter of the shaft. This is not theory. It is what average outcome measurements from comparable shots into real tissues show. It is a graphic demonstration of the importance of shaft drag as a factor in the overall resistance force when penetrating real tissues.

It is tempting to advise that one use as small a shaft diameter as possible, but recent testing is highly suggestive that other factors may also be at play. In the recent tests, shafts of identical materials and nearly equal mass, but of various profiles, were tested. All were tested at the same distance (20 yards), from the same bow, and with the same broadhead.

The results were, to say the least, of interest. Averaging the results from all comparable shots, the frequency of shafts with a tapered profile out-penetrating those with either parallel or barrel tapered profile was extremely high. A definite tendency was manifest.

Of note, the tapered shafts averaged about 50 to 70 grains less mass than either the parallel or the barrel tapered shafts. They also had a larger diameter at the point just back of the broadhead’s ferrule than either the parallel or tapered shafts, though ALL the shafts still had a diameter (just back of the broadhead) which was less than the broadhead’s ferrule diameter.

What the tapered shafts did have was a significantly higher percentage of weight forward of center (high FOC) and a shaft profile that became steadily smaller in diameter towards the rear of the shaft - a ‘reverse inclined plane’ which, in theory, might result in a lower overall shaft drag factor. It is also a feasible hypothesis that the lower mass towards the rear of the tapered shaft arrow may cause less shaft flexion, reducing resistance.

A new series of study ‘focal points’, designed to isolate only the FOC as a variable between the arrows physical structure, are planned. How much of the (consistently significant) difference in outcome penetration was due to the high FOC and how much to shaft profile or reduced flexion of the shaft? Only time will tell.

(8) Shaft and Broadhead Finish. Test data indicates that both a shaft’s finish and a broadhead’s ‘finish’ has a noteworthy effect on penetration. A very 'slick' finish on a shaft increases penetration, as it reduces the ‘coefficient of friction’ between shaft and tissues.

In soft tissues, recent test data is also highly suggestive that such metal finishes as Teflon coating aids a broadhead’s penetration through soft tissues, though a broadhead's finish appears to have very little, if any, significant effect on an arrow’s (or broadhead’s) ability to penetrate hard tissues (bone).

Undoubtedly, as terminal arrow performance is tested further, new information will be learned. As it stands now, the forgoing is the best I can recommend, and be assured it correctly reflects the outcome results relative to arrow penetration.

All of the above factors are things over which the bowhunter has control. The field evidence clearly shows that wise equipment selection does result in increased lethality of the hunting arrow. All that remains for the bowhunter to do is sharpen his or her shooting and hunting skills!

I hope the forgoing provides some insight into the penetration characteristics of arrows, and provides some practical applications for the bowhunter. For those interested in calculating the momentum and/or kinetic energy of their own arrows, here are the formulas in a simple to use format:

Formulas:

Momentum = Mass x Velocity

225218

In other words, momentum equals the arrow’s mass, measured in grains, multiplied by the arrow’s velocity, expressed in feet per second, and then divided by 225218. The resultant answer will be expressed in slug-feet per second.

Kinetic Energy = ½ Mass x Velocity²

225218

This says, the kinetic energy equals one-half the arrow’s mass, expressed in grains, multiplied by the arrow’s velocity (expressed in feet-per-second), then multiplied by the arrow’s velocity again, and all of that is then divided by 225218. The answer will be expressed in foot-pounds.

The denominator in the above equations, 225218, converts the arrow’s physical weight, measured in grains, into pounds, and also factors in the gravitational constant (g_c). There are 7000 grains per pound. The gravitational constant is 32.174 feet per second per second. Thus, 7000 x 32.174 = 225218.

Author's Note: A special "Thanks" to O. L. Adcock for his review and comments regarding bow efficiency and to Erik Beiergrohslein for his professional review of the accuracy of all Physics formulas and calculation, as well as the exactitude of their application(s) in the above document.